QUADRATURE DU CERCLE

Les constructeurs médiévaux pouvaient-ils réellement effectuer la quadrature du cercle ? On la dit impossible ! D’ailleurs, pour leurs calculs, comment auraient-ils pu extraire la racine carrée de Pi !

L’étude des églises médiévales montre pourtant que les bâtisseurs du moyen-âge savaient sans problème transformer un carré en un cercle de même surface alors que, effectivement, l’opération est depuis longtemps considérée comme impossible !
Mathématiquement parlant, il est vrai, elle ne peut pas être effectuée de façon exacte puisque π est un nombre incommensurable. La question est donc de comprendre comment les bâtisseurs médiévaux surent obtenir des résultats extraordinairement précis alors qu’ils ne connaissaient ni la valeur de π, ni les nombres décimaux, ni ne pouvaient effectuer de calculs tant soit peu compliqués ! C’est peut-être justement en raison de ces impossibilités qu’ils surent pratiquer… l’impossible quadrature !

Passer d’un cercle à un carré (ou d’un carré à un cercle) de même surface est, par nature, du domaine de la géométrie et … géométriquement cette opération se révèle fort simple. Pour le comprendre, il suffit de changer de point de vue, d’oublier les calculs et de s’intéresser non plus à π mais à Ø, le Nombre d’or. Ces deux proportions n’ont pourtant rien de commun !
Elles sont connues depuis l’Antiquité, connues mais non calculées car, à l’époque, non calculables ! Seules des approximations étaient envisageables.
Archimède, utilisant le théorème de Pythagore, a su montrer que la valeur de π était comprise entre deux limites. Il put écrire  :

223/71 < π < 22/7

D’où la valeur de 22/7 souvent attribuée par simplification au nombre π.
Les savants grecs ou leurs successeurs ne pouvaient pas, non plus, extraire la racine carrée de 5 qui intervient dans la formule du Nombre d’or. Ils montrèrent certainement la même détermination à essayer de mettre cette proportion sous une forme fractionnaire approchée et, s’intéressant à son carré, ils surent apparemment très tôt que les 6/5ème de ce carré était compris entre les mêmes limites que π. En effet, il leur était très facile de montrer que :

223/71 étant inférieur à 267/85, pour nos anciens, les deux valeurs étaient similaires et donc “interchangeables“ !

Pour effectuer les transformations d’un carré en cercle ou d’un cercle en carré, ils n’avaient pas besoin de calculer de surface car la quadrature se révélait géométriquement possible ! Rien n’est plus simple en effet que de tracer deux segments en proportion du Nombre d’or ou de son carré…
La transformation géométrique du cercle en un carré de même surface (ou l’opération inverse) découle directement de cette sorte d’identité et des propriétés des triangles rectangles. L’opération est simple et rapide. L’écart sur construction est de 1/100.000ème, autant dire négligeable !
Prenons le cas de la transformation d’un carré en un cercle de même surface, puisqu’il s’agit de l’opération qui était effectuée lors de la fondation des édifices religieux.

 

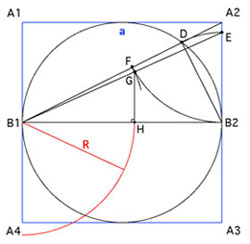Partant du carré A1, A2, A3, A4 :
Joindre B1, milieu de A1A4, à A2.
Tracer le cercle inscrit dans le carré. La droite B1A2 coupe le cercle en D.
Tracer un arc de cercle de centre B2 passant par D. Il coupe le côté A3A2 en E.
Tracer l’arc de cercle B2F de centre A2. F étant sur B1A2.
Joindre B1 à E.
Puis tracer un arc de cercle de centre B1 passant par F. Cet arc coupe B1E en G.
Abaisser la perpendiculaire issue de G sur B1B2.
B1H est égal au rayon du cercle cherché.

La transformation d’un cercle en un carré de même surface est tout aussi rapide.